Fibonacci et $\phi$

En tant qu’utilisateur de Youtube, je suis récemment tombé sur la vidéo The Infinite Pattern That Never Repeats par Veritasium. Et à un moment, (précisément 14:55), il explique la relation entre la suite de Fibonacci et le golden ratio.

The ratio of one fibonacci number to the previous one approaches the golden ratio

– Derek Muller

Mais ne serait-ce pas quelque chose que nous pourrions observer simplement avec un peut de python ?

Python

Il décidé d’écrire la fonction fibo qui afficherais les n premières valeurs de la suite:

def fibo(n):
    print(1)
    prev = 1
    actual = 1
    for i in range(n):
        print(actual)
        tmp = actual
        actual += prev
        prev = tmp

Si on essaye avec 5, on se retrouve avec:

>>> fibo(5)
1
1
2
3
5
8

Maintenant, ajoutons un paramètre supplémentaire qui va permettre d’effectuer un rapport entre les deux dernières valeurs et en afficher le résultat:

def fibo(n, f=lambda p, r: p / r):
    print(f"i: 0, f: 1, r: {f(0, 1)}")
    prev = 1
    actual = 1
    for i in range(n):
        print(f"i: {i}, f: {actual}, r: {f(actual, prev)}")
        tmp = actual
        actual += prev
        prev = tmp

Si on essaye avec 5 et la fonction qui permet de faire le rapport entre les deux, on obtient:

>>> fibo(5)
i: 0, f: 1, r: 0.0
i: 0, f: 1, r: 1.0
i: 1, f: 2, r: 2.0
i: 2, f: 3, r: 1.5
i: 3, f: 5, r: 1.6666666666666667
i: 4, f: 8, r: 1.6

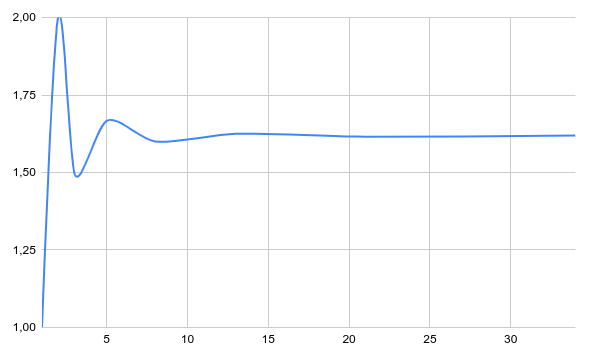
On peut observer que l’on se rapproche de la valeur de $\phi$ qui vaut $\phi \approx 1.6180339887…$. On peut d’ailleurs l’approximer facilement:

>>> (1 + 5 ** 0.5) / 2
1.618033988749895

D’autre part, si on utilise la fonction que j’ai écrite, on peut observer que le résultat converge vers $\phi$ rapidement mais qu’il faut attendre la 39 ième itération avant de voir la version arrondie de python:

>>> fibo(40, f=lambda a,b: a/b)
i: 0, f: 1, r: 0.0
i: 0, f: 1, r: 1.0
i: 1, f: 2, r: 2.0
i: 2, f: 3, r: 1.5
i: 3, f: 5, r: 1.6666666666666667
i: 4, f: 8, r: 1.6
i: 5, f: 13, r: 1.625
i: 6, f: 21, r: 1.6153846153846154
i: 7, f: 34, r: 1.619047619047619
i: 8, f: 55, r: 1.6176470588235294
i: 9, f: 89, r: 1.6181818181818182
i: 10, f: 144, r: 1.6179775280898876
i: 11, f: 233, r: 1.6180555555555556
i: 12, f: 377, r: 1.6180257510729614
i: 13, f: 610, r: 1.6180371352785146
i: 14, f: 987, r: 1.618032786885246
i: 15, f: 1597, r: 1.618034447821682
i: 16, f: 2584, r: 1.6180338134001253
i: 17, f: 4181, r: 1.618034055727554
i: 18, f: 6765, r: 1.6180339631667064
i: 19, f: 10946, r: 1.6180339985218033
i: 20, f: 17711, r: 1.618033985017358
i: 21, f: 28657, r: 1.6180339901755971
i: 22, f: 46368, r: 1.618033988205325
i: 23, f: 75025, r: 1.618033988957902
i: 24, f: 121393, r: 1.6180339886704431
i: 25, f: 196418, r: 1.6180339887802426
i: 26, f: 317811, r: 1.618033988738303
i: 27, f: 514229, r: 1.6180339887543225
i: 28, f: 832040, r: 1.6180339887482036
i: 29, f: 1346269, r: 1.6180339887505408
i: 30, f: 2178309, r: 1.6180339887496482
i: 31, f: 3524578, r: 1.618033988749989
i: 32, f: 5702887, r: 1.618033988749859
i: 33, f: 9227465, r: 1.6180339887499087
i: 34, f: 14930352, r: 1.6180339887498896
i: 35, f: 24157817, r: 1.618033988749897
i: 36, f: 39088169, r: 1.618033988749894
i: 37, f: 63245986, r: 1.6180339887498951
i: 38, f: 102334155, r: 1.6180339887498947
i: 39, f: 165580141, r: 1.618033988749895
i: 40, f: 267914296, r: 1.618033988749895